Analysis of THIN-WALLED TUBULAR STRUCTURES

Objective:                                                                                                                                To analyze the stresses produced in thin-walled tubular structures under torsion. So let us first discuss that what is torsion.

Actually torsion refers to twisting of a member about its longitudinal axis when it is loaded by couples.

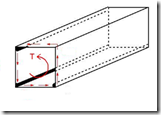
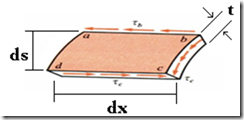
After interpreting the basic concept of torsion let us move to a situation in which a thin walled tubular structure, with arbitrarily shaped cross sectional area, is loaded by couples as shown in figure.

Before analyzing the stress distribution in thin-walled tubular structure following assumptions can simplify the situation a lot. The member is cylindrical i.e., cross section does not vary along length. Wall thickness is small as compared to cross sectional dimensions.

Now cut out an element between two cross sections. This element is acted upon by shear stresses on the cross section along edge. As the thickness of wall is very small so the variation of shear stresses along the thickness is negligible. But how stresses varies along the cross section must be determined.

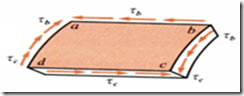
Again cut out a rectangular element by making two longitudinal cuts. Shear stresses varies as we move from ‘b’ to ‘c’ along x-section. Let shear stress is denoted by τb and τc at ‘b’ and ‘c’ respectively.

 

Shear Forces at faces ‘ab’ and ‘cd’ must be equal in magnitude to satisfy the equilibrium. Balancing the forces acting on longitudinal faces we get

τb tbdx = τc tcdx

Fb = Fc

τb tb = τc tc

above relation holds for each and every point of structure. Hence

τb tb = τc tc = constant

This constant quantity is known as shear flow and is denoted by ‘f’. So where thickness is large stresses are low and vice versa.

Applied Torque

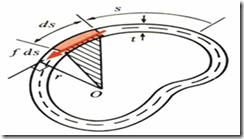
Consider a cross sectional element of length ‘ds’. Moment of the force ‘fds’ equals to torque acting on this element. Hence

dT = r fds

Total torque acting on x-section is obtained by integrating ‘dT’ as follows

T = ∫ dT = f ∫ r ds

∫ r ds, represents twice the area of shaded triangle. Hence

∫ r ds = 2Am

T = 2fAm

So now the shear flow in terms of applied torque is given as follows:

f = τ t = T/2Am

Similarly shear stresses in term of applied torque is given as follows:

τ = T/2tAm

As our structure is under torsion so there must exists some value of angle of twist.

 

Now the strain energy density of a small element is given as follows:

du = τ2/2G

So strain energy is given by

dU = τ2 (t ds dx)/2G

The above eqn. may be written as

dU = f2(dsdx/t)/2G

After integrating and putting the value of shear flow we get strain energy:

U = T2L / 8 G Am2 ∫ ds / t

 

How to get rid of ∫ ds / t ?

Through experimental analysis and using some advanced techniques we can define it in terms of torsion constant as follows:

J = 4Am2 / ∫ ds / t

So eqn. for strain energy becomes

U = T2L/2GJ

Work done by applied torque is equal to strain energy gain by thin-walled tubular structure. So

TΦ/2 = T2L/2GJ

Or

Φ = TL/GJ

Which is the equation to determine angle of twist for a torsionally loaded thin-walled tubular structure.

Now a little examination of the torsion formula :

Φ = TL/GJ

leads us to an important conclusion. If we replace the parameters in above equation by the corresponding parameters of any geometric x-section then the ‘J’ represents the polar moment of inertia of that body.

At beginning we assume that the thickness of tubular structure is very small but the ratio of radius and thickness must not exceed the value of 60 to avoid the buckling of our structure i.e., for a hollow bar with a length of 6m, the thickness must be 0.1m or above 0.1m. If anywhere in the bar thickness is less than 0.1m then reinforcement is needed there to avoid buckling.

r / t <= 60

(Courtesy of Engr. Ammar Aziz)