Prediction of Temperature distribution within Aluminium Alloy chip during orthogonal turning process

 

By: Engr. Ammar Aziz, Engr. Zohaib Hassan, Engr. Ahmad Bilal, Engr. Ali Hassan
COMSATS University of Science and Technology Sahiwal, Pakistan

Abstract
In this paper, a numerical model based on finite difference method is presented to predict chip temperature field in orthogonal turning process. Orthogonal turning can be studied by modeling the heat transfer between tool and chip at tool-rake face contact zone. The mathematical model and simulation results, presented here, are in satisfactory agreement with experimental temperature measurement reported in the literature.

1-  Preparing Numerical Model
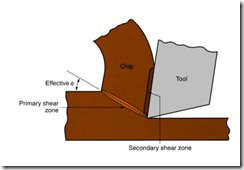
First of all consider the orthogonal turning process. Heat is generated within the chip due to its interaction with the tool. This heat generation is sub-divided into primary heat generation zone and secondary heat generation zone, as shown in the following figure:

Here ‘phi’ is the shear angle. It is the angle of the shear plane with the horizontal axis.

Rate of heat generation, per unit depth of cut within primary shear zone is given by:

Rate of heat generation within secondary shear zone is given by:

Average temperature rise of chip per unit depth of cut due to shearing:

This temperature rise is used as a boundary condition at the point shown in the figure:

Finite Difference Method and Derivative Concept:
Before proceeding to further modification, it is first necessary to clear that what is the meaning of a derivative and why we are relating it with finite difference concept. Also what does mean by partial derivative?

Meshing of our chip with 25 nodes

First law of thermodynamics implementation
Supposing a control zone within the mesh and applying the law of conservation of energy there we get:

According to Fourier’s law of heat conduction:

Substituting the values from Fourier’s law into heat balance equation we get:

Now by using the concept of Taylor series expansion about a point….

Approximating partial derivatives using forward and backward difference simultaneously, we get:

So our final model is ……

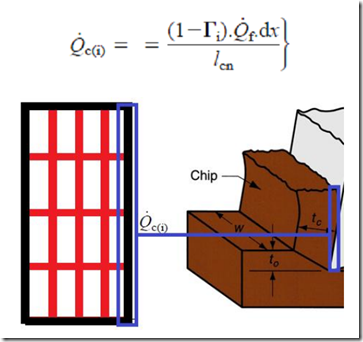
Heat flow in differential chip control zone from the frictional heat source is:

So heat generation array can be constructed by putting the value from above formula into all entries of last column and putting the value of heat generated in primary zone, in last row. All the entries except which described above are zero because here there is no heat generation as shown in the following figure:

 
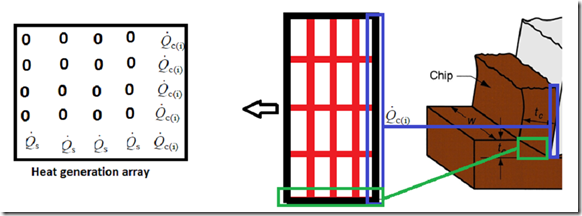
At last we determine the coefficients matrix which is obtained by solving the final model equation for each node of the chip and determining the coefficients through algebraic manipulations.

The purpose of above picture is to show you something interesting. As we write
the equation for each node the coefficients jump to next variable by one step. So if we try to write the above equations in matrix form than the matrix of
coefficients contain the entries which move diagonally. Siedal algorithm is best
to write the matrix of this type. The inverse of coefficient matrix is when multiplied by the heat generation array then we get the temperature distribution array which is our goal.

 
Plot of temperature against the distances along the edges of the chip in MATLAB:

Contour Plot:

Simulation of chip:
Solid works 2012 is used to accomplish the simulation of chip.

Description
Prediction of temperature distribution within chip of Aluminium. The tool which is used for turning process is made up of ‘C2 WC’.

Meshing…………..

Comment: The results are very close to those which are practically observed