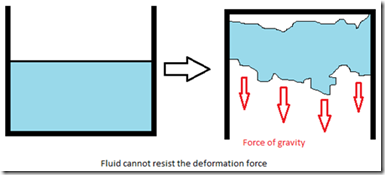
Actually water is a fluid and we know that a fluid cannot resists the deformation force i.e., it flows under the action of force. So we might expect that its shape will change continuously as long as the force is applied.
Let us first see that what is a water turbine and what is its use. So that we can deduce that what are the possible modifications whose introduction can play positive role in our investigation process of measuring and analyzing the velocity and pressure for installation of water turbine.
The most basic purpose of a water turbine is to convert the potential energy of water (as well as kinetic energy of water) into electrical energy through a series of steps.
Before further proceeding, it is also important to know that what is meant by potential and kinetic energy of water.
We know that it is the intrinsic property of every massive body to attract each other by a force whose magnitude is governs by a particular law. Similarly the earth also attracts every other massive body (like water) through certain amount of force. So when water attains some height we might expect that this is done by working against the force of gravity. This work on the water in height attaining process develops a potential within the raised water to work on its surrounding by losing its height. This property is known as gravitational potential energy.
Now let us move to kinetic energy. We know that it is the intrinsic property of every massive body to resist in its change of state; either it is state of rest or state of uniform motion with respect to a particular frame of reference. So when a massive body is moving with some speed then it resists anything which tries to resist its motion. The amount of resistance offered by moving water is also corresponds to kinetic energy. So when water is flowing with some speed then the kinetic energy of that flowing water impels it to work on anything which resists its flow.
So now we are clear that what is the basic idea of potential energy and kinetic energy of water.
In simple words we can say that energy possessed due to height is known as potential energy of water and energy possessed due to speed is known as kinetic energy of the water.
So these properties help us to use the water for the production of electrical energy through water turbine.
As we are going to explore the pressure profile for installation of water turbine it is necessary to know that what is meant by pressure of water. We know that the molecules of a fluid behave dynamically i.e. the molecules are free to move relative to each other. We might expect that due to this dynamic behavior, molecules may collide with each other and also with the confining boundary. Due to collision of molecules with the confining boundary a force equal to rate of change of momentum of that molecule is exerted upon the boundary. This force per unit area of confining boundary is known as the pressure of the water. This pressure may be dynamic or static depending upon whether water is moving or not respectively.
After knowing about the meaning of pressure of water, let us move to another concept known as pressure head. As we are dealing with the installation of a water turbine so this concept is very important for us. To know about pressure head let us investigate a situation in which a liquid of density ‘ℓ’ is poured into a vertical tube of x-sectional area ‘A’, until the tube is filled to a height ‘h’.
So, volume of liquid is given by
Volume = h A
It implies mass of liquid is
Mass = volume × density = h A ℓ
As we discussed earlier that earth, being a massive body, attracts all other massive bodies in his gravitational field. This force with which the earth attracts the other body is known as the weight of that body. So here the weight of the liquid exert a force ‘F’ on the base of the tube which is given by
F = mass × gravitational acceleration = m g = h A ℓ g
So pressure of the liquid is given by
P = F / A = h A ℓ g / A = h ℓ g
As we know that water is commonly treated as incompressible substance. So we can assume that the density of water is not changing during its interaction with the water turbine machinery and from above formula it becomes clear that the pressure may be quoted in terms of height ‘h’, the head of the liquid. This concept is referred as pressure head and it plays the key role in defining the efficiency and other parameters during the installation of a water turbine.
From above discussion we are inferred that more is the head of the water more is the pressure exerted by the water at the base. So it impels us to choose a location for the installation of water turbine where a reasonable head is available.
After knowing that what we are going to do, let us move to the mechanism on which water turbine works so that we can analyze the role of pressure and velocity of water to make the installation of turbine perfect.
As we know that water moves from high altitude to low altitude in the form of rivers under the action of gravitational force of earth. There are two ways to utilize the energy of that water. First one is to directly put a mechanism in front of streams of flowing water so that water can work on that mechanism by losing its kinetic energy, and second one is to block that flow by some constraint to gain the pressure head, so that water can work on the mechanism by losing its potential energy.
Commonly it is the second case which is preferable for the installation of water turbine. From previous discussion we see that pressure at the bottom of the water is directly proportional to the height of the head available there. You may conclude that it is very easy job to calculate the pressure by just measuring the head available there according to the formula, which we derived earlier
P = F / A = h A ℓ g / A = h ℓ g
Where
‘h’ represents the head available there
‘ℓ’ represents density of water and
‘g’ represents acceleration due to gravity.
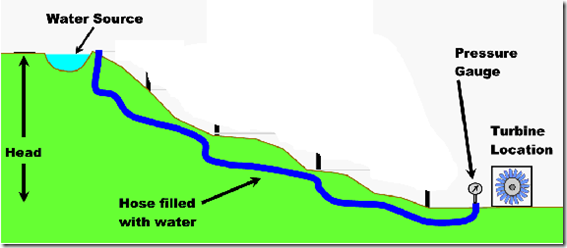
You may be forced to suppose that as the water is an incompressible fluid so pressure only depends upon the height or head available there. But the measurement of the head is one of the most challenging tasks during the installation of water turbine. Review that the head is actually the water pressure, created by the difference in elevation between the intake of your pipeline and your water turbine. This difference in elevation can be measured as the vertical distance between the intake of your pipeline and your water turbine by using an altimeter. But this method is not too much accurate. For accuracy the method of “Direct height measurement” is used.
This method of measuring head requires an assistant. Take a tall poll with graduated measurements. For example a measuring tape affixed with a 6 to 7 meters long PVC pipe works well. The method is illustrated in the following figure.
After each measurement, move the transit, or person with the sight level, to where the pole was, and begin again by moving the pole further downhill toward the generator site. Keep each transit or sight level setup exactly level, and make sure that the measuring pole is vertical. Take detailed notes of each measurement and the height of the level. Then, add up the series of measurements and subtract all of the level heights to find total head.
Another accurate method is the “water pressure measurement method”. Take one or more garden hoses or lengths of flexible plastic tubing to measure head. Run the hose (or tubing) from your proposed intake site to your proposed turbine location. If you attach multiple hoses together, make sure that each connection is tight and leak free. Attach an accurate pressure gauge to the bottom end of the hose, and completely fill the hose with water. Make sure that there are no high spots in the hose that could trap air. You can flush water through the hose before the gauge is connected to force out any air bubbles.
If necessary, you can measure total head over longer distances by moving the hose and taking multiple readings. Keep in mind, however, that there is less than 1/2 psi difference for every vertical foot. Except for very steep hillsides, even a 100-foot hose may drop only a few vertical feet. The chance for error significantly increases with a series of low-head readings. Use the longest possible hose, along with a highly accurate pressure gauge.
After determining the head by using any of these methods another aspect highlights in front of us. Actually during the flow of water through intake of pipeline to turbine the friction plays an important role in reducing the pressure of the water more than usual as we calculated through our methods. It is also important to note that longer pipelines, smaller diameters, and higher flows create greater friction. So we must take into account the frictional loses, due to friction of water with the pipelines and the machinery of turbine, during the estimation of pressure head.
There is another aspect which highlights in front of us and that is when water flows from intake of the pipeline to turbine it still feels some additional resistance other than the resistance due to friction between pipeline and other components of turbine. Actually when some quantity of water is added to intake of pipeline, there is a resistance due to the pressure of the fluid that already exists in the pipe. Hence we must exert a force on water to overcome that resisting pressure. So it is very important to keep this factor also in mind during the calculation of pressure.
The life is not easy still. Actually when water strikes the turbine blades then another phenomenon highlights itself. This phenomenon is known as back pressure. Actually when water strikes with the blades of turbine then it exerts a pressure on the turbine as a result of which turbine also exerts an opposite and equal pressure on the water which greatly reduce net pressure across the turbine. So keep this in mind during the calculation of pressure head otherwise measurements are uncertain.
Keep in mind that as the time passes away or due to change in environmental conditions, the head of a water turbine may loses its height. So keeping this aspect in mind the pressure is analyzed at three heads which are classified as; high, low and medium heads. So another modification to pressure measuring technique is to take the weighted average of all the three pressures described above.
After the determination of correct way to measure the pressure across the water turbine and analyzing its role in mechanism of water turbine let us divert our intentions to velocity profile of water for the installation of water turbine.
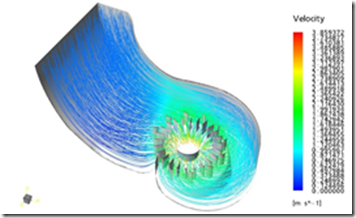
Actually the water in dam retained the gravitational potential energy. When the water enters from intake of pipeline and moves to turbine its gravitational energy is gradually changed into kinetics energy and flow work. Depending upon the geometry of the pipeline and the velocity with which water is moving through the pipeline the flow may be steady or turbulent. It is the part of turbine designing process to design the pipelines of a water turbine such that the flow remains steady. But when water strikes with the blades of the turbine the flow becomes turbulent or chaotic. So if we have to measure the flow rate of water through the pipelines then it is not recommended that after taking the initial velocity as zero, take the final velocity at the point of collision between water and turbine blades because it is nearly impossible to analyze the turbulent flow by using ordinary techniques. There is one method to do so. This method comprises of dividing the whole flow into a large number of streamlines and then simulating them by using super computers.
It is customary to define the efficiency of turbine in terms of following four parameters:
1- Flow rate
2- Head
3- Power output
4- Specific weight of water
Actually it is very important to measure the flow rate. But as we see earlier that it is very difficult to analyze the flow at turbine exit because of the conversion of flow from steady state to turbulent state. Also another important point is that after working on turbine the water exits from a tube known as draft tube. Here another problem occurs. The flow of water is converted into a very complex type of flow known as vortex flow. This flow is very difficult to analyze so if possible then design draft tube such that this type of flow doesn’t occurs, otherwise simulate this flow on super computers to get nearly accurate results.
Keep in mind the friction between the water and pipeline during the estimation of flow rate otherwise calculations are uncertain to great extent.
The best method to estimate the change in velocity of flowing water is by using law of conservation of energy.
According to it the total mechanical energy of fluid with mass ‘m’ and pressure ‘P’, moving with velocity ‘v’, at a height ‘h’ from our reference point, and having density equal to ‘ℓ’ is given by:
Mechanical energy = kinetic + potential + flow work
= mv2/2 + mgh + mP/ℓ
By rearranging and considering water as incompressible liquid the above expression becomes
m (v2/2 + hg + P/ℓ) = constant
Expressing the above expression for two states, we get
(v12 – v22)/2 + (h1 – h2)g + (P1-P2)/ℓ = 0
This expression is known as Bernoulli’s equation
According to law of conservation of energy the sum off all these terms remain constant throughout the pipeline. But unfortunately the friction between the pipeline and water results in loss of energy. So keep the frictional effect in mind during applying law of conservation of energy for the calculation of velocity.
There is another factor which plays an important role during the calculation of flow of water through the pipelines. This factor is ‘viscosity’. Actually when water is moving, its constituent layers move over one another. This movement results in friction between the layers. Each layer tends to pull its slower neighbor along with him but the slower layer tends to act as a brake on the higher velocity layer. This frictional interaction between layers is characterized by viscosity. Actually law of conservation of energy assumes that the flowing water is ideal i.e., there is no frictional loses between the layers. But that is not true for practical situations. So keep this in mind during the calculation of flow from law of conservation of energy to avoid uncertainty.
So now Bernoulli’s equation may be written as
V12/2 + h1g + P1/ℓ = v22/2 + h2g + P2/ ℓ + F12
Where F12 is the losses due to friction
Calculations of the energy in flowing water rely upon the Bernoulli equation, which represents the total energy as the sum of the velocity head, the pressure head, and an elevation relative to some fixed datum. The change in energy is equal to the change in this sum. Bernoulli derived one of the three familiar expressions of energy as:
Hv = V2/2g
Where:
– Hv is velocity head
– V is velocity
– g is the acceleration of gravity
But there is one problem. Use of average velocity yielded an incorrect estimate of total kinetic energy of water.
So another scientist named Gaspard Gustavo de Carioles formulated the expression by introducing a correction factor to Bernoulli’s equation as follows:
Hv = aVavg2/2g
Introduction of this correction factor reduces the uncertainty in calculation of velocity profile.








No comments:
Post a Comment