COMBINED LOADING

PRACTICALLY IT CAN BE OBSERVED THAT STRUCTURAL MEMBERS / COMPONENTS ARE REQUIRED TO RESIST MORE THAN ONE TYPE OF LOADING. FOR EXAMPLE, A SHAFT IN TORSION MAY ALSO BE SUBJECTED TO BENDING, OR A BEAM MAY BE SUBJECTED TO THE SIMULTANEOUS ACTION OF THE BENDING MOMENTS AND AXIAL FORCES. THE STRESS ANALYSIS OF A MEMBER SUBJECTED TO SUCH LOADING CONDITIONS (COMBINED LOADINGS) CAN BE CARRIED OUT BY SUPERIMPOSING THE STRESSES DUE TO EACH LOAD ACTING SEPARATELY. HOWEVER, SUPERIMPOSING CAN ONLY BE PERFOMED IF THE STRESSES ARE LINEAR FUNCTIONS OF THE LOADS AND IF THERE IS NO INTERACTION EFFECTS BETWEEN VARIOUS LOADS. SUCH TYPE OF SITUATION CAN ONLY BE ACHIEVED IF THE DEFLECTIONS AND ROTATIONS OF THE STRUCTURES ARE SMALL. ANALYSIS BY THE PROCESS OF SUPERIMPOSING BEGINS WITH THE DETERMINATION OF THE STRESSES DUE TO THE AXIAL FORCES, TORQUES, SHEAR FORCES, AND BENDING MOMENTS. AFTER DETERMINATION THESE STRESSES ARE COMBINED TO OBTAIN THE RESULTANT STRESSES, AFTER WHICH THE STRESSES ACTING IN INCLINED DIRECTIONS ARE INVESTIGATED BY STRESS TRANSFORMATION EQUATIONS. FINALLY THE PRINCIPAL STRESSES AND MAXIMUM SHEAR STRESSES DUE TO COMBINED LOADING ARE DETERMINED. IN BRIEF THE FOLLOWING THREE-STEP PROCEDURE WILL BE USEFUL IN SOLVING FOR STRESSES DUE TO COMBINED LOADING

1. DETERMINE THE INTERNAL RESULTANTS

THIS INVOLVES DRAWING FREE-BODY DIAGRAM AND WRITING EQUILIBRIUM EQUATIONS AS HAD BEEN DISCUSSED IN CASE OF INDETERMINATE STRUCTURES.

2. CALCULATE THE INDIVIDUAL STRESSES

FORMULAS AS LISTED BELOW ARE USED TO COMPUTE THE STRESS DISTRIBUTIONS THAT RESULT FROM THE VARIOUS STRESS RESULTANTS.

STRESS RESULTANT	SYMBOL	FORMULA
NORMAL FORCE	F	σ = F/A
TORSIONAL MOMENT	T	τ = Tρ / Ip
BENDING MOMENT	M	σ = My/I
TRANSVERSE SHEAR FORCE	V	τ = VQ / It

3. COMBINE THE INDIVIDUAL STRESSES

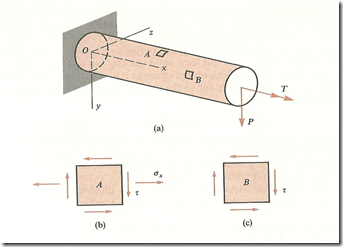
THIS STEP GENERALLY INVOLVES ALGEBRICALLY SUMMING LIKE STRESSES AND IN MOST CASES PRINCIPAL STRESSES AND MAXIMUM SHEAR STRESSES ARE CALCULATED. CONSEQUENTLY, EITHER THE ADEQUACY OF THE DESIGN IS CONFIRMED, OR IF THE STRESSES ARE TOO LARGE OR TOO SMALL DESIGN CHANGES NEEDED ARE IDENTIFIED. TO ELABORATE THIS DEFINED MECHANISM OF ANALYSIS, LET US CONSIDER A SOLID CIRCULAR CANTILEVER BAR. THIS BAR IS LOADED AT THE FREE END BY A TWISTING COUPLE “T” AND A LATERAL LOAD “P” WHICH CAUSES BENDING. THESE TWO LOADS PRODUCE A BENDING MOMENT (M), A SHEAR FORCE (V), AND A TWISTING COUPLE (T) AT EVERY X-SECTION OF THE STRUCTURE, EACH OF WHICH PRODUCES STRESSES ACTING OVER THE CROSS SECTIONS.

MOREOVER, BENDING MOMENT (M), SHEAR FORCE (V) AND TWISTING COUPLE (T) PRODUCE STRESSES ACTING OVER THE CROSS SECTIONS OF THE STRUCTURES. NOW IF WE ISOLATE STRESS ELEMENT “A” AT THE TOP OF THE BAR, IT CAN BE OBSERVED THAT THIS ELEMENT IS SUBJECTED TO BENDING AND SHEAR STRESSES WHICH CAN BE CALCULATED BY THE FOLLOWING RELATIONSHIPS:

σx = M r/ I AND τ = T r / Ip

IT CAN ALSO BE OBSERVED THAT AT THE TOP OF THE ELEMENT THERE ARE NO SHEAR STRESSES ASSOCIATED WITH SHEAR FORCE “V”. THUS A PLANE STRESS SITUATION IS OBTAINED. AFTER DETERMINING THE VALUES OF “σx” AND “τ”, WE CAN DETERMINE THE STRESSES ON AN ELEMENT ROTATED THROUGH ANY DESIRED ANGLE. THEREFORE, THE MAXIMUM AND MINIMUM NORMAL STRESSES AT POINT “A”, IN OTHER WORDS THE PRINCIPAL STRESSES, AND ALSO THE MAXIMUM SHEAR STRESS CAN OBTAINED BY THE FOLLOWING RELATIONSHIPS:

σ1,2 = σx /2 ± √(σx/2)² + τ²

τmax = √(σx/2)² + τxy²

THESE CALCULATED MAXIMUM VALUES OF STRESSES CAN BE COMPARED WITH THE ALLOWABLE NORMAL AND SHEAR STRESSES WHILE CHECKING THE ADEQUACY AND RELIABILITY OF BAR. IT MUST ALSO BE OBSERVED THAT THE STRESSES ARE LARGEST WHEN THE ELEMENT “A” IS LOCATED AT THE FIXED END OF THE BEAM WHERE THE BENDING MOMENT HAS ITS MAXIMUM VALUE. HENCE THE TOP OF THE BEAM AT THE SUPPORT IS ONE OF THE CRITICAL POINTS WHERE THE STRESSES MUST BE INVESTIGATED. ANOTHER CRITICAL POINT IS ON THE SIDE OF THE BAR AT THE NEUTRAL AXIS . AT THIS POINT THE BENDING STRESS IS ZERO BUT THE SHEAR STRESS PRODUCED BY THE SHEAR FORCE “V” HAS ITS LARGEST VALUE. THIS MEANS THAT THIS IS THE STATE OF PURE SHEAR WITH RESULTANT SHEAR STRESS CONSISTING OF TWO PARTS; FIRST THE SHEAR STRESS DUE TO THE TORQUE AND THE OTHER DUE TO THE SHEAR FORCE “V”. SHEAR STRESS DUE TO THE TORQUE “T” AND SHEAR STRESS DUE TO THE SHEAR FORCE ”V” APPLIED ON THE SHAFT CAN BE OBTAINED BY THE FOLLOWING RELATIONSHIPS: (SOLID SHAFT IN CASE OF SHEAR FORCE)

τ1 = Tr/Ip AND τ2 = 4V / 3A

TOTAL SHEAR STRESS = τ = τ1 + τ2

AS THE PRINCIPAL STRESSES OCCUR ON PLANES AT 45º TO THE AXIS AND HAVE THE SAME MAGNITUDES AS THE SHEAR STRESS ITSELF. THEREFORE,

σ1,2 = ±τ

THESE MAXIMUM NORMAL AND SHEAR STRESSES SHOULD BE COMPARED WITH THOSE OBTAINED FOR ELEMENTS AT THE TOP AND BOTTOM OF THE BAR IN ORDER TO ASCERTAIN THE ABSOLUTE MAXIMUM STRESSES FOR USE IN DESIGN. IN FACT THE VARIETY OF PRACTICAL SITUATIONS IS SEEMINGLY ENDLESS, SO IT NOT WORTHWHILE TO DERIVE SPECIFIC FORMULAS FOR DESIGN USE. INSTEAD IN CASE OF COMBINED LOADING EACH STRUCTURE IS ANALYZED AT VARIOUS CRITICAL POINTS AND THE RESULTS ARE COMPARED. WHEN SELECTING THE POINTS TO BE INVESTIGATED, IT IS NATURAL TO CHOOSE THOSE LOCATIONS WHERE EITHER THE NORMAL OR THE SHEAR STRESSES ARE MAXIMUM.